Matrizenrechnung
Die Matrizenrechnung hat viele Anwendungen. In diesem Kapitel lernst du die Rechenoperationen kennen, die man mit Matrizen durchführen kann. Von besonderer Bedeutung ist die Matrizenmultiplikation und die Darstellung von Linearen Gleichungssystemen in Matrix/Vektor-Schreibweise. Verschiedene Anwendungen der Matrizenrechnung werden in separaten Kapiteln behandelt.


m13v0485 Bei dieser Übung sollst du eine Matrix aus Matrixelemente konstruieren, für die eine Zuordnung angegeben ist. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0157 In diesem Video wird eine grundlegende Rechenoperation von Matrizen vorgestellt, die für viele Aufgabentypen ganz wichtig ist - die Matrizenmultiplikation. | auf teilen
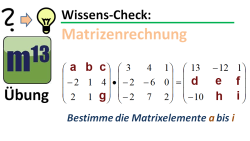

m13v0281 Dies ist eine Aufgabe, mit der du überprüfen kannst, ob du die Matrizenmultiplikation verstanden hast - auch das Lösen von Linearen Gleichungssystemen musst du für die Bestimmung einiger der gesuchten Matrixelemente beherrschen. | Arbeitsblatt zum Download | auf teilen


m13v0626 Im Allgemeinen ist die Matrizenmultiplikation nicht kommutativ. Für eine vorgegebene Matrix A sollst du nun alle Matrizen B finden, so dass die Matrizenmultiplikation kommutativ ist. | Arbeitsblatt zum Download | auf teilen


m13v0481 In dieser Videolektion lernst du die Einheitsmatrix auch Identitätsmatrix genannt kennen. Multipliziert man eine Matrix A mit der Einheitsmatrix, so erhält man wieder die Matrix A als Ergebnis. Wie die Einheitsmatrix aussieht und welche Voraussetzungen erfüllt sein müssen, damit die Identität der multiplizierten Matrix beibehalten wird, erfährst du in diesem Video. | auf teilen
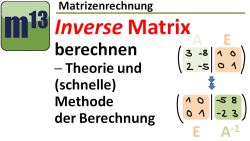

m13v0482 In diesem Lektionsvideo lernst du die inverse Matrix kennen. Hat man eine quadratische Matrix gegeben und multipliziert man diese mit der (ebenfalls quadratischen) inversen Matrix, so erhält man die Einheitsmatrix. In diesem Video wird ausführlich gezeigt, wie man eine inverse Matrix von Hand berechnet. Auch wird die Berechnung mit dem GTR (TI-nspire) vorgemacht. | auf teilen


m13v0546 Bei dieser Aufgabe, die so ähnlich als Abitur-Aufgabe gestellt wurde, geht es darum, dass man eine Inverse Matrix zu einer gegebenen Matrix M bestimmen soll, und außerdem soll man einen Fixvektor dieser Matrix M bestimmen. Diese Aufgabe ist als hilfsmittelfreie Aufgabe ausgelegt. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
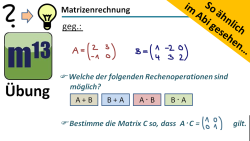

m13v0612 Dies ist ein Video aus der Serie "So ähnlich im Abi gesehen" über grundlegende Rechenoperationen von Matrizen. Zum einen soll die Durchführbarkeit von Rechenoperationen mit Matrizen unterschiedlichen Formats beurteilt werden; des Weiteren soll eine Inverse Matrix berechnet werden. | Arbeitsblatt zum Download | auf teilen