Exponentialfunktionen
Exponentialfunktionen spielen eine sehr wichtige Rolle bei der Modellierung von Wachstums- und Zerfallsprozessen. Wenn sich ein Bakterium immerzu teilt und aus einem Bakterium werden 2, dann 4, dann 8, dann 16 usw., dann ist dies ein Beispiel für exponentielles Wachstum. Beim Zerfall einer radioaktiven Substanz hat man es hingegen mit exponentieller Abnahme bzw. Zerfall zu tun.
Zunächst wirst du Funktionen vom Typ f(x)=c·ax kennenlernen. Später werden wir und dann mit einer besonderen Exponentialfunktion, der natürlichen Exponentialfunktion f(x)=ex beschäftigen.
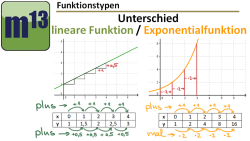
m13v0420 Früher haben wir ja schon lineare Funktionen zur Beschreibung von Zunahme- bzw. Abnahmeprozessen kennengelernt. In diesem Kapitel lernst du zusätzlich exponentielle Zunahme und Abnahme kennen. In diesem Video werden die grundlegenden Unterschiede herausgearbeitet. | auf teilen
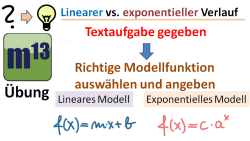
m13v0415 Aufbauend auf das vorige Video m13v0420 kannst du mit Hilfe dieser Übung überprüfen, ob du den Unterschied zwischen linearem bzw. exponentiellen Wachstum/Abnahme verstanden hast. Es werden Wachstums-/Abnahmeprozesse beschrieben, denen der Typus linear bzw. exponentiell zugeordnet werden soll. | Skript zum Download | auf teilen
m13v0172 Eine Exponentialfunktion vom Typ f(x)=c·ax ist durch zwei Punkte eindeutig bestimmt. In diesem Video wird gezeigt, wie man aus den Koordinaten zweier Graphenpunkte die zugehörige Funktionsgleichung ermitteln kann. | auf teilen
m13v0448 Nachfolgend zum Video m13v0172 soll hier eine weitere Methode zur Bestimmung einer Exponentialfunktion vom Typ f(x)=c·ax vorgestellt werden. | auf teilen
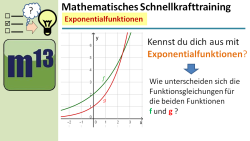
m13v0599 Bei diesem Video aus der Serie "Mathematisches Schnellkrafttraining" geht es darum, Aussagen über den Verlauf des Graphen einer Exponentialfunktion anhand der im Funktionsterm vorkommenden Parameter zu machen. | Skript zum Download | auf teilen
m13v0364 In diesem Übungsvideo werden die Exponentialfunktionen des Typs f(x)=k·wx betrachtet. Hier soll man jetzt den Graphenverlauf skizzieren in Abhängigkeit der Werte von k und w. So eine ähnliche Aufgabe kam in Österreich in der Matura-Klausur vor. | Skript zum Download | auf teilen
Da die Funktionsgleichung f(x)=c·ax vier Größen enthält, gibt es vier Aufgabentypen, bei denen jeweils drei der Größen bekannt sind und man die vierte bestimmen soll.
- Funktionswert f(x) an gegebener x bestimmen
- Startwert bzw. Anfangsbestand c bestimmen
- Wachstums-/Zerfallsfaktor a bestimmen
- Exponent x bestimmen. Häufig ist dies die Zeit, weshalb die Variable dann oft mit t benannt ist.
m13v0216 Typische Aufgaben zum Thema Kapitalwachstum und Zinseszins - Wie man Anfangskapital, Endkapital, Zinssatz und Anlagedauer berechnet. | auf teilen
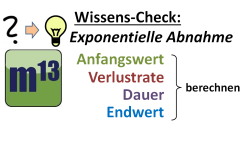
m13v0217 Zweites Übungsvideo zum exponentiellen Wachstum und Zerfall - diesmal geht es um Abnahme- und Zerfallsprozesse. Bestimme die fehlenden Werte (Anfangswert, Endwert, Verlustrate, Dauer). | auf teilen
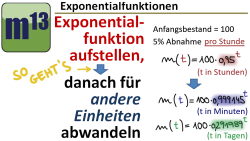
m13v0445 In diesem Video wird gezeigt, wie man eine Exponentialgleichung so anpasst, dass man die Variable in anderen Einheiten verwenden kann. Hat man z.B. eine Exponentialfunktion für die stündliche Abnahme eines Bestands gegeben, so kann man die Funktion abwandeln, so dass man anstatt Stunden auch Minuten oder Tage als Zeiteinheit verwenden kann. | auf teilen
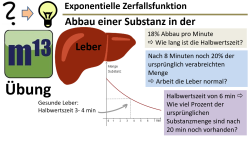
m13v0710 Dies ist eine klausurtypische Aufgabe, bei denen verschiedene Kompetenzen zu Exponentialfunktionen abgefragt werden: Berechnung der Halbwertszeit; Berechnung des Zerfallsfaktors und Bestimmung des Bestands zu einem bestimmten Zeitpunkt. | Skript zum Download | auf teilen
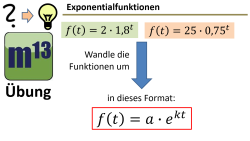
m13v0693 Bei dieser Übung sollst du eine Exponentialfunktion, die in der Form f(t)=a·bt gegeben ist, in das e-Funktion-Format f(t)=a·ekt umwandeln. | Skript zum Download | auf teilen
m13v0425 In diesem Übungsvideo geht es um die Transformation von Graphen von Exponentialfunktionen. In der einen Aufgabe sollst du zeigen, dass es zwei unterschiedliche Wege der Transformation (Verschieben bzw. Stauchen/Strecken) gibt, die zum selben Ergebnis führen. In der zweiten Aufgabe sollst du die einzelnen Schritte der Transformationen angeben, mit der man von einer Exponentialfunktion zu einer anderen Exponentialfunktion gelangt. | Skript zum Download | auf teilen
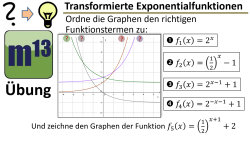
m13v0706 Eine klausurtypische Aufgabe, bei der du Funktionsgraphen den richtigen Funktionstermen zuordnen sollst. Außerdem sollst du den Graphen einer Gleichung ins Koordinatensystem einzeichnen. | Skript zum Download | auf teilen
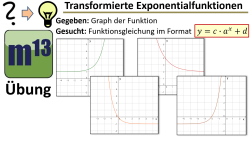
m13v0707 Bei dieser Übungsaufgabe sind Graphen von Exponentialfunktionen gegeben, und du sollst dazu die entsprechenden Funktionsgleichungen im Format y=c·ax+d angeben. Diese Aufgabe ist nicht ganz einfach, aber im Video wird eine zuverlässige Methode erklärt, mit der das Aufstellen der Funktionsgleichung schnell gelingt. | Skript zum Download | auf teilen
m13v0708 Bei diesen Aufgaben sollst du die Funktionsterme für Exponentialfunktionen des Typs f(x)=c∙ax aufstellen; verfügbar sind Angaben zur Verdopplungs- bzw. Halbwertszeit, Anfangsbestand und bekannter Graphenpunkte. | Skript zum Download | auf teilen
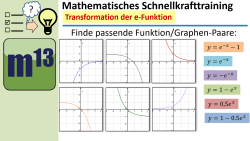
m13v0686 Wie gut kennst du dich mit Transformationsoperationen von Funktionen aus? Bei dieser Übungsaufgabe sollst du passende Paare von Funktionsterm und Funktionsgraph einander zuordnen. | Skript zum Download | auf teilen
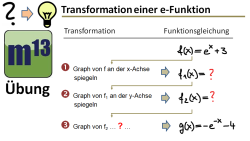
m13v0621 Eine Übung zur schrittweisen Transformation einer Ausgangsfunktion zu einer Zielfunktion. Die Schritte sind beschrieben, und du sollst die Gleichungen der Zwischenschritt-Gleichungen angeben. Für den letzten Schritt, sollst du die auch die Transformation beschreiben. | Skript zum Download | auf teilen
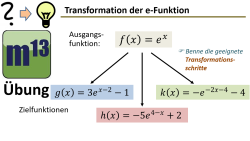
m13v0659 Bei dieser Übungsaufgabe sollst du eine geeignete Reihenfolge von Transformationsschritten aufstellen, mit denen sich die Ausgangsfunktion f(x)=ex in die angegebene Zielfunktion überführen lässt. | Skript zum Download | auf teilen
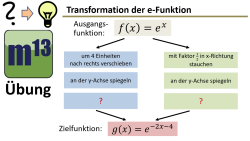
m13v0672 In dieser Übungsaufgabe soll der Frage nachgegangen werden, ob man die Reihenfolge der Transformationen verändern kann und dennoch zur selben Zielfunktion gelangt... | Skript zum Download | auf teilen
Die natürliche Exponentialfunktion / e-Funktionen
Bislang haben wir Exponentialfunktionen des Typs f(x)=c·ax betrachtet. Dabei war die Basis a eine positive Zahl, die für a > 1 exponentielles Wachstum und für 0 < a < 1 exponentiellen Zerfall beschreibt. Im Folgenden werden wir Exponentialfunktionen mit einer besonderen Basis betrachten. Diese Basis ist die Eulersche Zahl e. e ist eine irrationale Zahl (e ≈ 2,718). Was Exponentialfunktionen zur Basis e so besonders macht, und warum man mit den sogenannten e-Funktionen komfortabel rechnen kann, erfährst du in den folgenden Videos...
m13v0447 In diesem Video wird eine besondere Exponentialfunktion behandelt - die natürliche Exponentialfunktion mit der Basis e. e ist die Eulersche Zahl, näherungsweise 2,718. Hier wird gezeigt, dass es eine Exponentialfunktion gibt, deren Ableitungsfunktion mit der Ausgangsfunktion übereinstimmt: f(x)=e^x. Außerdem wird gezeigt, wie man einen Näherungswert für die Eulersche Zahl e ermitteln kann. Zur Herleitung von e benutzt man die Differentialquotienten-Definition der Ableitung. | auf teilen
m13v0667 Bei dieser Aufgabe sollst du am Funktionsterm erkennen, ob der Graph der Funktion eine exponentielle Zunahme oder Abnahme darstellt. Bei einigen Funktionstermen kommt in der Basis auch die Eulersche Zahl e vor. | Skript zum Download | auf teilen
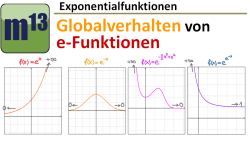
m13v0452 Den Verlauf der natürlichen Exponentialfunktion f(x)=ex sollte man kennen − äh, den muss man kennen!. Aber wie wird der Verlauf des Graphen durch den Exponenten beeinflusst, also wenn man es mit einer Funktion f(x)=eg(x) zu tun hat, wobei g(x) eine mehr oder weniger komplizierte Funktion sein kann − zum Beispiel eine ganzrationale Funktion?! In diesem Video wird es erklärt. Soviel sei verraten: Was immer auch passiert, es passiert oberhalb der x-Achse... | auf teilen
