Differentialrechnung I: Einführung in die Differentialrechnung
In diesem Abschnitt beginnt die Einführung in die Differentialrechnung, ein sehr wichtiges und umfangreiches mathematisches Konzept, das dich bis zum Abi begleiten wird.
Im Teil Differentialrechnung I wird der Stoff präsentiert, der üblicherweise in der Einführungsphase behandelt wird. Dies umfasst: (1.) Die Herleitung des Ableitungsbegriffs ausgehend von der mittleren Änderungsrate einer Funktion zur momentanen Änderungsrate. Die mittlere Änderungsrate wird über den Differenzenquotienten bestimmt und beschreibt die Änderung über ein Intervall. Durch die Grenzwertbildung, bei der das betrachtete Intervall unendlich klein wird, gelangt man von Differenzenquotienten zum Differentialquotienten und damit zur Ableitung. (2.) Herleitung und Anwendung der grundlegenden Ableitungsregeln. (3.) Verwendung der Differentialrechnung zur Funktionsuntersuchung. (4.) Bestimmung von Tangenten und Normalengleichungen.
In der Einführungsphase betrachtet man üblicherweise nur ganzrationale Funktionen und die trigonometrischen Funktionen Sinus und Kosinus. In dem späteren Kaptitel Differentialrechnung II wird der Stoff behandelt, der in der Qualifikationsphase dazukommt.
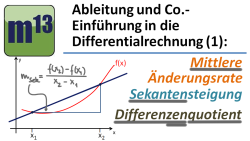

m13v0257 Bevor es mit der Differentialrechnung richtig losgeht, müssen wir zunächst über die mittlere Änderungsrate einer Funktion sprechen. Dies ist ein Wert, der beschreibt, wie sich der Verlauf eines Graphen auf einem Intervall - also zwischen zwei Graphenpunkten - ändert. Man legt dazu eine Gerade - die Sekante - durch die beiden Graphenpunkte und bestimmt deren Steigung mit Hilfe des sogenannten Differenzenquotienten. Du wirst sehen, dass die Begriffe mittlere Änderungsrate, Sekantensteigung und Differenzenquotient Synonyme für die gleiche Sache sind. | auf teilen


m13v0258 Im vorigen Video hast du den Differenzenquotient kennengelernt, mit dem man die mittlere Änderungsrate einer Funktion bestimmt. In diesem Video lernst du, wie man durch Verkleinerung des Intervalls allmählich zur momentanen Änderungsrate gelangt. Der Differenzenquotient geht dabei in den Differentialquotienten über. Dies führt zur Einführung des Ableitungsbegriffs. | auf teilen
Im Folgenden geht es um die konkrete Berechnung des Differentialquotienten - also der Ableitung. Von den beiden vorgestellten Methoden ist die h-Methode die häufiger in der Schule angewandte Methode.


m13v0029 Die sogenannte h-Methode zur Bestimmung der Ableitung an einer Stelle durch Grenzwertberechnung des Differentialquotienten. | auf teilen
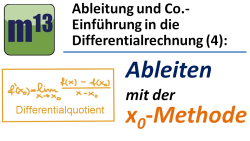

m13v0259 In diesem Video lernst du, wie man mit Hilfe der sogenannten x0-Methode die Ableitung einer Funktion berechnet. Du wirst sehen, dass man bei der Anwendung der x0-Methode üblicherweise eine Polynomdivision durchführen muss, um den Bruch zu vereinfachen und den Grenzwert berechnen zu können. An einem Beispiel wird das alles ausführlich vorgemacht. | auf teilen
Wenn ihr in der Schule einige ganzrationale Funktionen die Ableitungen mit Hilfe des Differentialquotienten (z.B. mit Hilfe der h-Methode) bestimmt habt, werdet ihr beim Vergleich von Ausgangs- und Ableitungsfunktion schon bald ein "Muster" erkennen. Aus diesem "Muster" lassen sich einige grundlegende Ableitungsregeln ableiten, mit denen man aber auch kompliziertere Funktionen, wie Wurzelfunktionen und einfache Bruchfunktionen ableiten kann... Die nächsten Videos behandeln diese Ableitungsregeln. Diese grundlegenden Ableitungsregeln sind sehr wichtig - absolutes Grundwissen der Oberstufenmathematik.

m13v0156 In diesem Video werden die grundlegenden Ableitungsregeln erklärt, die du bis zum Ende der Einführungsphase kennen solltes. Mit diesen Regeln kann man ganzrationale Funktionen ableiten. | auf teilen
Die grundlegenden Ableitungsregeln, die wir soeben für ganzrationale Funktionen besprochen haben, lassen sich sehr einfach für andere Funktionen ausdehen, die sich auch als Potenzfunktionen schreiben lassen: dies sind einfache Bruchfunktionen und Wurzelfunktionen.


m13v0192 In diesem Video wird gezeigt, wie du einfache Bruchfunktionen ableiten kannst, nachdem du sie in die Potenzschreibweise umgeschrieben hast. Diese Funktionen haben alle Grundkurs-Niveau. | auf teilen


m13v0195 In diesem Video wird gezeigt, wie du einfache Wurzelfunktionen ableiten kannst, nachdem du sie in die Potenzschreibweise umgeschrieben hast. Diese Funktionen haben alle Grundkurs-Niveau. | auf teilen


m13v0810 Für diese Aufgabe geht es darum, die erste und zweite Ableitung einer Reihe von Funktionen zu bestimmen. Obwohl die Funktionen auf den ersten Blick unterschiedlich oder sogar kompliziert wirken, lassen sie sich alle mit den grundlegenden Ableitungsregeln berechnen. Hierbei kommen die Summenregel, die Produktregel, die Faktorregel, die Potenzregel und die Konstantenregel zum Einsatz. | Arbeitsblatt zum Download | auf teilen
Wichtige Aufgabentypen zur Ableitung


m13v0319 In diesem Video werden zwei wichtige Aufgabentypen zu Ableitungen besprochen: 1) Wie ermittelt man die Steigung einer Funktion f an einer gegebenen Stelle? und 2) An welchen Stellen hat die Funktion f eine gegebene Steigung m? Weil diese Aufgabentypen dieselbe Sache von verschiedenen Seiten betrachten, wird dies schon mal gerne verwechselt. Dieses Video soll Klarheit bringen. Und das Gute ist: die Vorgehensweise ist dieselbe, egal, um welche Art von Funktion des sich handelt. | Arbeitsblatt zum Download | auf teilen
Funktionsuntersuchung mittels Ableitungen
In den nächsten Videos erfährst du, dass sich bestimmte Eigenschaften einer Funktion in bestimmten Eigenschaften in der Ableitungsfunktion widerspiegeln - und umgekehrt. Dazu vergleichen wir zunächst die Graphen von Funktionen mit den Graphen ihrer entsprechenden Ableitungsfunktionen. Die Beziehungen, die wir bei dieser Gegenüberstellung herausfinden, werden wir anschließend systematisch einsetzen, Funktionseigenschaften und charakteristische Punkte von Funktionen rechnerisch mit Hilfe von Ableitungen zu bestimmen.

m13v0200 In diesem Video wird gezeigt, wie man anhand des gegebenen Funktionsgraphen der Funktion f den Verlauf des Graphen der Ableitungsfunktion f' ermitteln kann. Dieses graphische Ableiten ist ein häufiger und wichtiger Aufgabentyp, weil hierdurch der Zusammenhang zwischen Funktion und Ableitung geübt werden kann. | Arbeitsblatt zum Download | auf teilen

m13v0201 In diesem Video geht es um die die Umkehrung des graphischen Ableitens. Es ist der Graph einer Ableitung f' gegeben und man soll einen Graphen einer möglichen Ausgangsfunktion f finden. | auf teilen


m13v0589 Bei dieser Übungsaufgabe aus der Serie "Mathematisches Schnellkrafttraining" musst du deine Kenntnisse zum graphischen Ableiten anwenden... | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0596 Eine weitere Aufgabe über den Zusammenhang von Funktionseigenschaften und Ableitungen bei ganzrationalen Funktionen. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0740 In diesem Video geht es um einen Aufgabentyp, der in Klausuren (auch in Abi-Klausuren!) regelmäßig vorkommt: man soll anhand vorgegebener Funktionseigenschaften − auch unter Einbeziehung der Ableitung − einen möglichen Graphen der Funktion skizzieren. | Arbeitsblatt zum Download | auf teilen


m13v0761 Bei dieser Aufgabe sollst du anhand von gegebenen Informationen über Monotonieverhalten und relativen und absoluten Extrempunkten einen möglichen Verlauf eines Funktionsgraphen skizzieren. | Arbeitsblatt zum Download | auf teilen

m13v0742 Um diese Aufgabe lösen zu können, musst du: (1.) den Verlauf von Grundfunktionen kennen; (2.) den Effekt der Transformation am Funktionsterm erkennen; und daraus (3.) das Steigungsverhalten der transformierten Funktion an gegebenen x-Stellen bestimmen können. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
Die nachfolgenden Videos behandeln, wie man spezielle Funktionseigenschaften (Monotonie, Krümmung) und charakteristische Punkte (relative Hoch-, Tief-, Sattelpunkte und Wendepunkte) mit Hilfe von Ableitungen berechnet. Zunächst gibt es jeweils ein Theorievideo, dann folgt ein Video mit Rechenbeispiel.

m13v0272 In diesem Video erfährst du, was man unter dem Monotonieverhalten einer Funktion versteht und wie man die erste Ableitung nutzen kann, das Monotonieverhalten einer Funktion zu untersuchen. | auf teilen

m13v0273 In diesem Video wird an mehreren Beispielen vorgemacht, wie man das Monotonieverhalten einer Funktion untersucht. | auf teilen

m13v0274 Dieses Video behandelt die Theorie der Extrempunktbestimmung mit Hilfe von Ableitungen. Hier wirst du die wichtigen Begriffe *notwendiges Kriterium* und *hinreichendes Kriterium* kennenlernen. | auf teilen


m13v0275 Hier wird die rechnerische Bestimmung von relativen Extrempunkten am Beispiel einfacher ganzrationaler Funktionen vorgemacht. | auf teilen


m13v0276 In diesem Video wird erklärt, was man unter dem Krümmungsverhalten einer Funktion versteht und wie man dies mit Hilfe der zweiten Ableitung untersuchen kann. Außerdem lernst du Wendepunkte als charakteristische Punkte eines Funktionsgraphen kennen, an denen sich das Krümmungsverhalten ändert. | auf teilen

m13v0277 In diesem Video wird an Beispielen vorgemacht, wie man Wendepunkte und das Krümmungsverhalten einer Funktion rechnerisch bestimmt. | auf teilen


m13v0278 Dieses Video fasst noch einmal übersichtlich zusammen, wie man mit Hilfe der ersten bis dritten Ableitung das Monotonieverhalten, relative Extrempunkte, Krümmungsverhalten und Wendepunkte einer Funktion bestimmen kann. | auf teilen
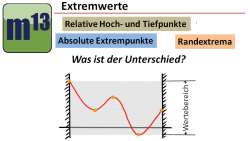

m13v0456 In diesem Video geht es um den Unterschied zwischen lokalen, relativen Extrema (mit waagerechter Tangente) und Extrema an den Rändern eines vorgegebenen Definitionsbereichs (sogenannte Randextrema). Randextrema müssen nicht unbedingt eine waagerechte Tangente haben, sie sind aber die höchsten bzw. niedrigsten Punkte auf einem betrachteten Intervall. | Arbeitsblatt zum Download | auf teilen
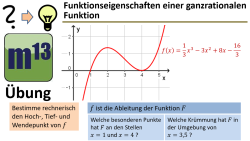

m13v0666 Eine typische Aufgabe zur Untersuchung von Funktionseigenschaften einer Funktion (bzw. Ihrer Stammfunktion) mittels der Auswertung der Ableitung. So ähnlich in vielen Klausuren gesehen... | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0787 In dieser Aufgabe analysierst du eine ganzrationale Funktion f, von der jedoch nur die Ableitungsfunktion gegeben ist. Du sollst die Monotonieintervalle von f bestimmen und die x-Stellen der Hoch- bzw. Tiefpunkte des Graphen ermitteln. Dabei stellt sich die Frage: Warum lässt die Untersuchung der Ableitungsfunktion keine direkten Rückschlüsse auf die genauen Punktkoordinaten der Extrempunkte der Ausgangsfunktion f zu? | Arbeitsblatt zum Download | auf teilen


m13v0809 In dieser Aufgabe untersuchst du das Monotonie- und Krümmungsverhalten einer Funktion mit einer anspruchsvollen Ableitung. Dabei trainierst du, Ableitungen korrekt zu berechnen und deren Vorzeichen zu analysieren, um Aussagen über die Eigenschaften der Funktion zu treffen. Tipp: Stelle die Ableitungen in faktorisierter Form dar ? das erleichtert dir die Analyse. | Arbeitsblatt zum Download | auf teilen


m13v0804 Dies ist eine Übungsaufgabe zur Untersuchung des Krümmungsverhaltens einer Funktion mithilfe der zweiten Ableitung. Während die Untersuchungsmethode dieselbe ist, unterscheiden sich die Funktionen hinsichtlich der anzuwendenden Ableitungsmethoden. | Arbeitsblatt zum Download | auf teilen


m13v0613 Ein Video aus der Serie "Mathematisches Schnellkrafttraining". Hier geht es darum, anhand von allgemeinen Aussagen über die Funktion f und ihrer ersten und zweiten Ableitung, einen möglichen Funktionsgraphen der Funktion f zu zeichnen. | Arbeitsblatt zum Download | auf teilen
Nachfolgend einige Videos zur Funktionsuntersuchung.


m13v0446 In diesem Video wird besprochen, wie viele Nullstellen, Extrempunkte und Wendepunkte man für eine ganzrationale Funktion vom Grad n erwarten kann und welcher Zusammenhang für die Anzahl dieser charakteristischen Punkte besteht. In diesem Video findest du Antworten auf typische Klausuraufgaben wie: Wie viele Wendestellen hat eine Funktion 3. Grades? Wie viele Extrempunkte kann eine Funktion 4. Grades haben? usw. | auf teilen


m13v0577 Bei dieser Aufgabe hast du für eine ganzrationale Funktion dritten Grades eine Wertetabelle für einige ausgewählte x-Werte für die Funktion sowie ihrer Ableitung gegeben. Zum einen sollst du Aussagen zu Extrempunkten machen, du sollst aber auch angeben, wie die Funktion zu verändern ist, damit sie genau zwei Nullstellen hat. Dies ist eine interessante Aufgabe, bei der dein Wissen über die Bedeutung der Ableitung und über die Transformation von Funktionsgraphen gefordert wird. Eine Aufgabe aus der Serie So ähnlich im Abi gesehen. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
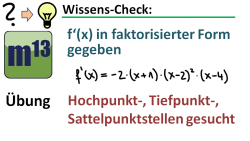

m13v0279 Auch bei dieser Übungsaufgabe soll man mit Hilfe der Ableitungsfunktion Aussagen über charakteristische Punkte wie Extrem- und Sattelpunkte gemacht in der Ausgangsfunktion f machen. In diesem Fall ist die Ableitungsfunktion in faktorisierter Form gegeben, was die Untersuchung sogar einfacher macht. | Arbeitsblatt zum Download | auf teilen


m13v0790 Bei dieser Aufgabe geht es um die Untersuchung einer ganzrationalen Funktion, die in faktorisierter Form gegeben ist. Die besondere Herausforderung besteht darin, die Ableitung mithilfe der Produktregel und der Kettenregel zu bilden. Anschließend werden die Nullstellen der Ableitung bestimmt, und du analysierst, ob es sich dabei um Hochpunkte, Tiefpunkte oder Sattelpunkte der Funktion handelt. Diese Aufgabe fördert dein Verständnis für die Ableitung und die Eigenschaften von Funktionsgraphen. | Arbeitsblatt zum Download | auf teilen
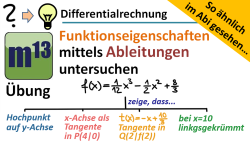

m13v0374 In diesem Übungsvideo geht es um die Untersuchung von Funktioneigenschaften (Extrempunkte, Tangente, Krümmung) mit den Mitteln der Differentialrechnung. Dies ist ein Video aus der Serie "So ähnlich im Abi gesehen"; eine ähnliche Aufgabe wurde im Abi des Landes Bayern von 2018 gestellt. | Arbeitsblatt zum Download | auf teilen


Klicke hier und werde Level 2 (mathehoch13 Club-Member)-Kanalmitglied. Damit erhältst Vorab-Zugang zu allen Videos in der Produktionspipeline.
m13v0807


m13v0584 Eine weitere Aufgabe aus der Serie "Mathematische Schnellkrafttraining" bei es darum geht, Eigenschaften einer Funktion aus Eigenschaften ihrer Ableitung zu ergründen. | Arbeitsblatt zum Download | auf teilen
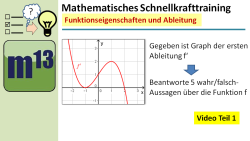

m13v0629 Bei diesem Aufgabe aus der Serie "Mathematisches Schnellkrafttraining" ist der Graph der ersten Ableitung der Funktion f" gegeben, und du sollst fünf Aussagen über die Ausgangsfunktion f bewerten, ob diese jeweils richtig, falsch oder unter bestimmten Bedingungen richtig ist. Beachte, dass es zu dieser Aufgabe noch eine Erweiterung mit fünf weiteren Fragen gibt (Video m13v0630). | Arbeitsblatt zum Download | auf teilen
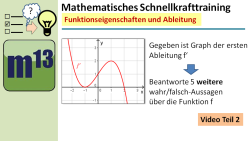

m13v0630 Dies ist der zweite Teil der "Mathematisches Schnellkrafttraining"-Aufgabe mit fünf weiteren Aussagen zu einem Graphen einer ersten Ableitung, die wieder jeweils mit "wahr", "falsch" oder "unter bestimmten Umständen wahr" zu bewerten sind. Hier sind deine Kenntnisse über den Zusammenhang von Funktionseigenschaften und Ableitung sowie zu ganzrationalen Funktionen gefragt. Teil 1 dieser Aufgabe gibt es im Video m13v0629. | Arbeitsblatt zum Download | auf teilen
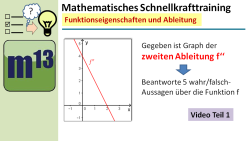

m13v0616 Eine weitere Aufgabe aus der Serie "Mathematisches Schnellkrafttraining". Es geht um die Interpretation des Graphen der zweiten Ableitung, um Aussagen über die Ausgangsfunktion f zu beurteilen. Den zweiten Teil findest du unter der Aufruf-ID m13v0617. | Arbeitsblatt zum Download | auf teilen
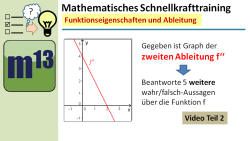

m13v0617 Dies ist der zweite Teil der Aufgabe mit fünf weiteren Aussagen über den Zusammenhang zwischen zweiter Ableitungsfunktion und Ausgangsfunktion. Der erste Teil hat die Aufruf-ID: m13v0616. | Arbeitsblatt zum Download | auf teilen
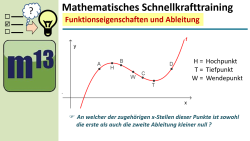

m13v0652 In diesem Video geht es über den Zusammenhang zwischen Funktionseigenschaften und der ersten und zweiten Ableitung. Eine Aufgabe aus der Videoserie "Mathematisches Schnellkrafttraining". | Arbeitsblatt zum Download | auf teilen


m13v0796 In der Mittelstufe hast du die Scheitelpunktform der quadratischen Funktion kennengelernt: f(x)=a(x-d)2+e. In dieser Form kannst du die Koordinaten des Scheitelpunkts S(d|e) direkt ablesen. In dieser Aufgabe wendest du dein neues Wissen über die Funktionsuntersuchung mittels Ableitung an, um zu bestätigen, dass der Scheitelpunkt die Koordinaten S(d|e) hat. Diese Übung stärkt dein Verständnis für quadratische Funktionen und vertieft deine analytischen Fähigkeiten im Umgang mit Extremstellen. | Arbeitsblatt zum Download | auf teilen
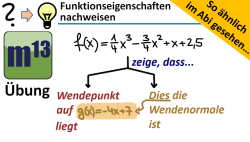

m13v0375 Bei dieser Aufgabe soll man zeigen, dass der Wendepunkt einer ganzrationalen Funktion auf einer gegebenen Gerade liegt und dass diese Gerade die Normale durch den Wendepunkt ist. Außerdem soll man den Graphen der Funktion verschieben und eine Gleichung der verschobenen Gleichung angeben. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0760 Bei dieser Aufgabe sollst du eine besondere Eigenschaft einer ganzrationalen Funktion nachweisen, die die Lage der Wendepunktstellen im Verhältnis zu den Nullstellen betrifft. Dabei musst du deine Kenntnisse zur Untersuchung von Funktionseigenschaften mithilfe von Ableitungen und zur Nullstellenbestimmung ganzrationaler Funktionen einsetzen. | Arbeitsblatt zum Download | auf teilen
Tangente und Normale
Ein häufiger Aufgabentyp stellt die Bestimmung der Gleichung von Tangenten und Normalen dar. Tangenten sind Geraden, die sich im Berührpunkt perfekt an den Graphen einer Funktion anschmiegen. Dieses perfekte Anschmiegen kommt dadurch zustande, dass Tangente und Funktion im Berührpunkt dieselbe Steigung haben. Eine Normale ist eine Gerade, die im Berührspunkt senkrecht zur Tangente verläuft.


m13v0202 In diesem Video wir ausführlich an einem Beispiel erklärt, wie man die Tangentengleichung aufstellt. | auf teilen


m13v0203 In diesem Video wird die allgemeine Tangentengleichung hergeleitet. | auf teilen
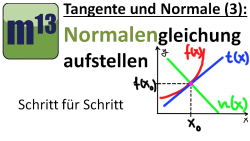

m13v0204 In diesem Video wird gezeigt, wie man die Gleichung einer Normalen aufstellt. Die Normale steht im Berührpunkt senkrecht zur Tangenten. | auf teilen


m13v0205 In diesem Video wird die allgemeine Normalengleichung hergeleitet. | auf teilen

m13v0416 Achtung: Zu diesem Video ist eine Korrekturanmerkung verfügbar. | auf teilen


m13v0583 Bei dieser Aufgabe aus der Serie "So ähnlich im Abi gesehen" geht es um die gegenseitige Lage einer Parabel und einer Geraden. Die Parabelfunktion ist eine Funktionenschar in Abhängigkeit eines Parameters. Nun sollst du den Parameter so bestimmen sollst, dass die Gerade zur Tangente wird.. | Arbeitsblatt zum Download | auf teilen


m13v0442 In diesem Video wird ein wichtiger Aufgabentyp behandelt: Das Aufstellen der Gleichung einer Wendetangente. Eine Wendetangente ist eine Tangente durch den Wendepunkt. Dazu muss man (1.) den Wendepunkt der Funktion bestimmen, dann (2.) die Steigung der Funktion an der Wendestelle über die Ableitung ermitteln und schließlich (3.) aus Punkt und Steigung die Geradengleichung aufstellen. Im Video wird das Vorgehen am Beispiel einer ganzrationalen Funktion vorgemacht, doch im Prinzip lässt sich das Verfahren auf jeden Funktionstyp übertragen. | auf teilen

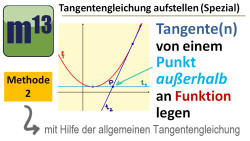
m13v0443 In diesem Video wird gezeigt, wie man von einem Punkt aus, der selbst nicht auf dem Graphen der Funktion liegt, Tangenten an die Funktion legt und die zugehörigen Tangentengleichungen bestimmt. In einem weiteren Video wird eine weitere Methode gezeigt. | auf teilen


m13v0460 In diesem Video wird gezeigt, wie man nachweisen kann, dass bei einer ganzrationalen Funktion 3. Grades der Wendepunkt immer genau zwischen den Extrempunkten liegt (sofern des Extremstellen gibt). Dazu wird eine allgemeine Funktion 3. Grades betrachtet und dann mittels der ersten bis dritten Ableitung auf Extrem- und Wendestellen untersucht... | auf teilen

m13v0636 Eine Aufgabe, bei der es um die Fläche geht, die im I. Quadraten von der Tangente an den Graphen einer Funktion mit den Koordinatenachsen eingeschlossen wird. Für die Funktion f(x)=1/x ergibt sich ein interessanter Zusammenhang, den du beweisen sollst. | Arbeitsblatt zum Download | auf teilen


m13v0435 Das Newton-Verfahren ist ein numerisches Verfahren zur näherungsweisen Berechnung von Nullstellen. Es beruht auf die wiederholte Anwendung einer Iterationsformel, bei dem das Ergebnis der Rechnung wieder in die Formel eingesetzt wird. So kommt man ausgehend von einem Startwert (und wenn der Algorithmus funktioniert) immer näher an die wahre Nullstelle heran. In dem Video wird die Formel hergeleitet und die Anwendung vorgemacht. | auf teilen


m13v0436 In dem ersten Video dieser Serie hatten wir die Herleitung des Newton-Verfahrens zur näherungsweisen Bestimmung der Nullstelle einer Funktion besprochen. In diesem Video besprechen wir die Fälle, bei denen das Newton-Verfahren nicht funktioniert und schauen uns an Beispielen und Graphen an, was genau dann nicht funktioniert. In Prüfungen wird immer wieder gerne nach solchen Fällen gefragt. | auf teilen
Die folgenden Videos sind Übungsaufgaben zur weiteren Vertiefung des oben behandelten Stoffs.


m13v0036 Überprüfe Dein Wissen - "Mathematisches Schnellkraft-Training" Beantworte die Fragen zum Zusammenhang von Funktionseigenschaften und Ableitung Nach Vorstellung der Aufgabenstellung kannst du das Video pausieren und die Aufgabe lösen; anschließend kannst du dir die Lösung anschauen. | auf teilen


m13v0037 Teil 2 des "mathematischen Schnellkrafttrainings"... | auf teilen


m13v0038 Teil 3 des "mathematischen Schnellkrafttrainings" ... | auf teilen

m13v0218 Übungsaufgabe aus der Einführungsphase zu den Themen: Nullstellen, Extrempunkt bestimmen, Sekantengleichung und Tangentengleichung aufstellen. Diese Aufgabe könnte so zum Beispiel in der Zentralen Klausur am Ende der Einführungsphase im hilfsmittelfreien Teil gestellt werden. | Arbeitsblatt zum Download | auf teilen

m13v0219 Übungsaufgabe aus der Einführungsphase zu den Themen: Nullstellen, Extrempunkt bestimmen, Sekantengleichung und Tangentengleichung aufstellen. Diese Aufgabe könnte so zum Beispiel in der Zentralen Klausur am Ende der Einführungsphase im hilfsmittelfreien Teil gestellt werden. | Arbeitsblatt zum Download | auf teilen


m13v0431 In diesem Video wird gezeigt, wie man prüft, ob sich die Graphen zweier Funktionen an einer vorgegebenen Stelle/einem vorgegebenen Punkt berühren. Dies ist eine typische Aufgabe zur Anwendung der Ableitung. Zwei Funktionen berühren sich an einer Stelle x0, wenn dort ihre Funktionswerte und ihre Steigungen übereinstimmen. | auf teilen
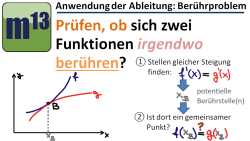

m13v0433 Nachdem in dem vorigen Video gezeigt wurde, wie man untersucht, ob sich zwei Graphen an einer gegebenen Stelle oder Punkt berühren, wird hier jetzt der allgemeinere Fall behandelt: Berührstellen bzw. -punkte von Grund auf Suchen und Berührtangente aufstellen. | auf teilen


m13v0654 Eine klausurtypische Aufgabe, bei der es um die Anwendung der Ableitung geht. Hier geht es insbesondere darum zu erkennen, welcher Rechenansatz zu verwenden ist, wenn nach der Steigung an einer bestimmten Stelle gefragt wird bzw. wenn gefragt wird, an welche(n) Stellen der Graph einer Funktion eine bestimmte Steigung hat. | Arbeitsblatt zum Download | auf teilen