m13v0604  Eine einfache Einstiegsaufgabe zur Berechnung der Wahrscheinlichkeit einer binomialverteilten Zufallsgröße. Hier kannst du prüfen, ob du den Zusammenhang zwischen Länge der Bernoulli-Kette, Trefferzahl und Trefferwahrscheinlichkeit verstanden hast. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf  teilen

 m13v0344  In diesem Video wird eine klassische Aufgabe aus dem hilfsmittelfreien Teil vieler Klausuren behandelt: Man hat einen Term zur Wahrscheinlichkeitberechnung angegeben und man soll das zugrundeliegende Ereignis beschreiben... | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf  teilen

 m13v0345  In diesem Video soll noch einmal geübt werden, wie man ausgehend von einer Problemstellung den Ansatz zur Berechnung der Wahrscheinlichkeiten aufstellt. Insbesondere werden auch die Schreibweisen der B- und F-Funktion und die zugehörigen Taschenrechner-Befehle binompdf und binomCdf behandelt. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf  teilen

 m13v0668  Ebenfalls ein häufiger Aufgabentyp im Themenkomplex Binomialverteilung: Zuordnung des richtigen Berechnungsterms zur Wahrscheinlichkeit eines gegebenen Ereignisses. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf  teilen

 m13v0723  Diese Aufgabe behandelt einen beliebten Aufgabentyp zur Binomialverteilung: Ein Berechnungsterm f�r die Wahrscheinlichkeit eines Ereignisses ist gegeben, und du sollst das zugeh�rige Ereignis angeben. Das besondere an dieser Aufgabe ist, dass du das Ereignis aus zwei Blickwinkeln formulieren sollst. | Arbeitsblatt zum Download | auf  teilen

 m13v0399  In diesem Video erfährst du, wie man eine Binomimalverteilung zu gegebener Bernoulli-Kettenlänge n und Trefferwahrscheinlichkeit berechnet und als Wahrscheinlichkeitsverteilungsdiagramm zeichnet. Außerdem wird auf die Verteilungsfunktion und den Zusammenhang der Binomialverteilung für Treffer- und Nieten-Wahrscheinlichkeit eingegangen. | Arbeitsblatt zum Download | auf  teilen

 m13v0580  In diesem Video geht es darum, dass du die richtigen Ansätze für die Berechnung von Wahrscheinlichkeiten beim Ziehen mit Zurücklegen anwendest. Zwei Fälle werden in dieser Aufgabe behandelt. Ein Video aus der Serie "So ähnlich im Abi gesehen". | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf  teilen

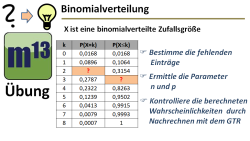
 m13v0619  Mit dieser Übungsaufgabe kannst du dein Verständnis überprüfen, was den Aufbau und den Zusammenhang zwischen der diskreten und der kumulierten Wahrscheinlichkeitsverteilungstabelle betrifft. Außerdem sollst du anhand der Wahrscheinlichkeiten in der Tabelle die Parameter n und p der zugrundeliegenden Binomialverteilung bestimmen. | Arbeitsblatt zum Download | auf  teilen

 m13v0453  In diesem Video aus der Serie "So ähnlich im Abi gesehen" geht es um den Umgang mit der Tabelle der kumulierten Binomialverteilung. Du sollst mithilfe der dieser Tabelle die Wahrscheinlichkeit einer Treffer-Einzelwahrscheinlichkeit bzw. die Wahrscheinlichkeit für ein Intervall von Trefferzahlen bestimmen. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf  teilen

 m13v0722  In diesem Video wird gezeigt, wie man bei der Berechnung von Wahrscheinlichkeiten vorgehen muss, wenn das oder die Trefferzahlenintervalle in Form einer Betragsungleichung angegeben sind. Dabei werden zwei verschiedene Fälle behandelt. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf  teilen

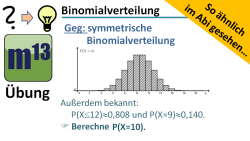
 m13v0618  Bei dieser Aufgabe kommt es darauf an, dass du teilweise gegebene Wahrscheinlichkeiten und die besonderen Eigenschaften einer symmetrischen Binomialverteilung geschickt anwendest, um eine gesuchte Einzelwahrscheinlichkeit zu bestimmen. Dies ist ein Video aus der Serie "So ähnlich im Abi gesehen". | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf  teilen

 m13v0543  Bei dieser Aufgabe ist eine Gleichung gegeben, die eine Beziehung zwischen zwei Einzelwahrscheinlichkeiten für eine binomialverteilte Zufallsgröße angibt, und die zugehörige Trefferwahrscheinlichkeit p, für die diese Beziehung zutrifft, ist zu bestimmen. Dies ist ein Video aus der Serie "So ähnlich im Abi gesehen". | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf  teilen

 m13v0695  Es gibt Situationen, bei denen man bei einem wiederholt durchgeführten Zufallsexperiments auf den Erfolg zu einem bestimmten Zeitpunkt wartet ? z.B. frühestens/spätestens/ genau im k-ten Durchgang. In dieser Übungsaufgabe geht es um die Berechnung von Wahrscheinlichkeiten für solche Ereignisse. | Arbeitsblatt zum Download | auf  teilen

 m13v0487  In diesem Video wird die Formel für den Erwartungswert ?=n·p einer binomialverteilten Zufallsgröße für die Fälle n=1,2,3 bei beliebigem p bestätigt. Eine allgemeine Herleitung der Formel geht über das Schulniveaus etwas hinaus. | Arbeitsblatt zum Download | auf  teilen

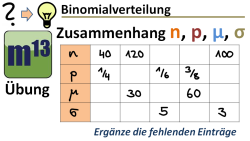
 m13v0401  In diesem Übungsvideo kannst du prüfen, ob du bei der Binomialverteilung den Zusammenhang zwischen n, p, mue und sigma kennst. Dabei ist n die Länge der Bernoulli-Kette, p die Trefferwahrscheinlichkeit, mue der Erwartungswert und sigma die Standardabweichung. Es sind jeweils zwei Parameter angegeben, die anderen beiden sollst du berechnen. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf  teilen

 m13v0602  Von einer Binomialverteilung (Verteilung 1) kennst du n und p. Jetzt sollst du eine andere Binomialverteilung (Verteilung 2) bestimmen, die denselben Erwartungswert hat wie Verteilung 1, aber ihre Standardabweichung soll das √1,5-fache betragen... Worin stimmen die Verteilungsgraphen von Verteilung 1 und Verteilung 2 überein, worin unterscheiden sie sich? | Arbeitsblatt zum Download | auf  teilen

 m13v0548  Bei dieser Aufgabe ist die Ereigniswahrscheinlichkeit für einen Treffer bei einem Bernoulli-Experiment mit n=3 zu bestimmen. Dazu benötigt man natürlich auch die Trefferwahrscheinlichkeit p, welche aber nicht direkt gegeben ist. Wohl kennt man den Erwartungswert ?=2. Mit gegebenem n und ? zuerst p bestimmen, um dann zu P zu gelangen ? darum geht es in dieser Aufgabe aus der Serie "So ähnlich im Abi gesehen". | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf  teilen

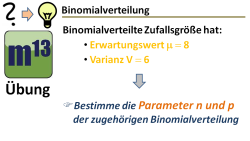
 m13v0647  Eine Übungsaufgabe, bei der du deine Kenntnisse über den Zusammenhang zwischen Erwartungswert, Varianz und den Parametern n und p einer Binomialverteilung überprüfen kannst. | Arbeitsblatt zum Download | auf  teilen

 m13v0648  Bei dieser Aufgabe musst du die Zusammenhänge der Parameter einer Binomialverteilung (n, p, μ und σ) kennen. Hier sind jetzt Erwartungswert μ und Standardabweichung σ gegeben, und - nachdem du daraus n und p bestimmt hast - sollst du die Wahrscheinlichkeit P(X≥1) berechnen. | Arbeitsblatt zum Download | auf  teilen

 m13v0538  In diesem Video werden ein paar typische hilfsmittelfreie Grundaufgaben zur Binomialverteilung behandelt: (1.) Berechnung von Erwartungswert und Standardabweichung; (2.) Identifizierung eines korrekten Berechnungsterms zur Berechnung einer Wahrscheinlichkeit und (3.) Bestimmung der Wahrscheinlichkeit für mindestens einen Treffer. | Arbeitsblatt zum Download | auf  teilen

 m13v0404  Eine Binomialverteilung ist durch die Parameter n (die Länge der Bernoulli-Kette) und p (der Trefferwahrscheinlichkeit) bestimmt. In diesem Video untersuchen wir, wie n und p den Verlauf des Verteilungsgraphen beeinflussen.  | auf  teilen

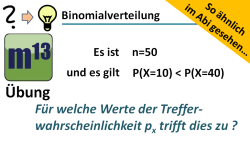
 m13v0567  Bei dieser Aufgabe aus der Serie "So ähnlich im Abi gesehen" geht es darum, dass du deine Kenntnisse über die Eigenschaften der Binomialverteilung in Abhängigkeit der Parameter n und p geschickt anwendest. Gegeben ist n=50; für welche Werte der Trefferwahrscheinlichkeit p gilt: P(X=10) > P(X=40) ? | Arbeitsblatt zum Download | auf  teilen

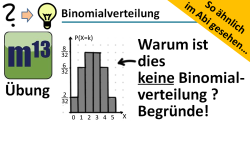
 m13v0466  Bei dieser Aufgabe soll untersucht werden, ob eine gegebene Wahrscheinlichkeitsverteilung tatsächlich eine Binomialverteilung ist oder nicht. Hier ist dein Wissen über Eigenschaften von Binomialverteilungen gefragt. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf  teilen

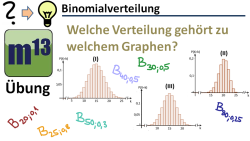
 m13v0402  Mit diesem Übungsvideo kannst du überprüfen, ob du verstanden hast, wie die Parameter n und p die Gestalt des Graphen der Binomialverteilung beeinflussen. Hier sind drei Graphen gegeben und du sollst die richtige Binomialverteilung zuordnen. | Arbeitsblatt zum Download | auf  teilen

 m13v0427  Dies ist ein Übungsvideo zur Anwendung der Binomialverteilung beim Würfeln, speziell bei Aufgaben, wo nach der Wahrscheinlichkeit für "genau", "mindestens", "höchstens" soundso viele Sechsen gefragt wird. Dies sind beliebte Aufgaben für den hilfsmittelfreien Teil in Klausuren. | Arbeitsblatt zum Download | auf  teilen

 m13v0717  Bei diesem Video aus der Serie "So ähnlich im Abi gesehen" behandeln wir zwei Aufgabentypen: Erstens untersuchen wir, wie sich die Wahrscheinlichkeit bei wiederholten Bernoulli-Experimenten verändert, wenn wir bestimmte Ausgangsreihenfolgen, beispielsweise für zwei Treffer, mit der Wahrscheinlichkeit vergleichen, einfach irgendwie zwei Treffer zu erzielen. Im zweiten Abschnitt dieser Aufgabe geht es darum, für eine gegebene Ereignisbeschreibung das richtige zugehörige Binomialwahrscheinlichkeits-Histogramm auszuwählen. | Arbeitsblatt zum Download | auf  teilen

 m13v0347  In diesem ersten Video erfährst, wie du die Wahrscheinlichkeit für Ereignisse berechnest, deren Trefferzahl k mit Vokabeln wie genau, mindestens, höchstens, von ... bis, weniger als, mehr als beschrieben wird. Punktwahrscheinlichkeiten werden mit der B-Funktion bzw. der GTR-Funktion binomPdf berechnet; kumulierte Wahrscheinlichkeiten werden über die F-Funktion bzw. mittels binomCdf berechnet.  | auf  teilen

 m13v0348  Ein sehr beliebter Aufgabentyp ist die sogenannte "dreimal-mindestens-Aufgabe", auch "mindestens-mindestens-mindestens-Aufgabe" genannt. Hierbei soll bestimmt werden, wie groß n mindestens sein muss, wenn man für mindestens einen Treffer einen Mindestwert einer Ereigniswahrscheinlichkeit fordert. Anders ausgedrückt: Wie groß muss n mindestens sein, damit P(X≥1) ≥ (gegebene Mindest-Ereigniswahrscheinlichkeit). Hier solltest du dir merken, dass die Lösung dieser drei-mal-mindestens-Aufgabe über die Gegenwahrscheinlichkeit 1-P(X=0) läuft, bei der man zunächst die Bernoulli-Formel aufstellt, die eine Exponentialgleichung liefert, die man dann über den Logarithmus löst...  | auf  teilen

 m13v0350  Wenn man nicht - wie im vorigen Video - den Spezialfall P(X?1) betrachtet, sondern die dreimal-mindestens-Aufgabe für P(X?k) erweitert, muss man das gesuchte n aus einer Tabelle mit kumulierten Wahrscheinlichkeiten ermitteln. Am beliebten Aufgabentyp "Überbuchung" wird dies vorgemacht... | auf  teilen

 m13v0353  Natürlich kann man bei gegebener Kettenlänge n und Trefferwahrscheinlichkeit p auch die benötigte Trefferzahl oder ein Trefferzahl-Intervall ermitteln, damit eine geforderte Ereigniswahrscheinlichkeit P erreicht wird. | auf  teilen

 m13v0356  Die Bestimmung der Trefferwahrscheinlichkeit klein p ist ebenfalls ein beliebter Aufgabentyp. Hier wird zunächst die Aufgabenformulierung einer dreimal-mindestens-Aufgabe behandelt. Dabei geht man über die Bernoulli-Formel und berechnet p durch Lösen einer Wurzel-Gleichung. | auf  teilen

 m13v0358  In diesem Video wird vorgemacht, wie man klein p graphisch mittels GTR bestimmt, durch Auftragen der binomcdf-Funktion in Abhängigkeit von p gegen die Grenzwahrscheinlichkeit.  | auf  teilen

 m13v0557  Bei dieser Aufgabe aus der Serie "So ähnlich im Abi gesehen" ist die Gleichung geben, mit der man den Parameter n einer Binomialverteilung bestimmen soll. Anhand dieser Gleichung sollst du die Aufgabenstellung rekonstruieren, die dieser Berechnung zugrunde liegt. Die Interpretation von Berechnungstermen oder Gleichungen ist ein relativ häufiger Aufgabentyp zu Binomialverteilungen. | Arbeitsblatt zum Download | auf  teilen

 m13v0680  Eine weitere Aufgabe aus der Serie "Mathematisches Schnellkrafttraining". Wieder mal geht es um die Mathematisierung einer Aussage. Findet du den geeigneten Berechnungsterm für den beschriebenen Sachverhalt? | Arbeitsblatt zum Download | auf  teilen

 m13v0597  In diesem Video wird ein häufiger Aufgabentyp zur Binomialverteilung behandelt: Es geht darum für eine Ereignisbeschreibung den passenden Berechnungsterm herauszufinden. Eine Aufgabe aus der Serie "Mathematisches Schnellkrafttraining". | Arbeitsblatt zum Download | auf  teilen

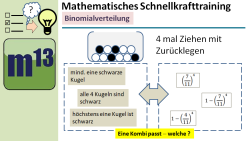
 m13v0598  Eine weitere Aufgabe aus der Serie "Mathematisches Schnellkrafttraining", wobei es darum geht, für ein beschriebenes Ereignis für eine binomialverteilte Zufallsgröße den richtigen Berechnungsterm für die Wahrscheinlichkeit herauszufinden. | Arbeitsblatt zum Download | auf  teilen

 m13v0572  Diese abiturtypische Aufgabe besteht aus zwei Teilen, die aufeinander aufbauen: zum einen die Ermittlung des Erwartungswertes einer Zufallsgröße und anschließend die Berechnung der Wahrscheinlichkeit eines Ereignisses mit binomialverteilter Zufallsgröße. Dieses Video aus der Serie "So ähnlich im Abi gesehen" wurde inspiriert durch die Abiklausur aus NRW im Jahr 2019. | Arbeitsblatt zum Download | auf  teilen

 m13v0603  Dies ist eine mehrteilige Anwendungsaufgabe zur Binomialverteilung. Es geht um das Ziehen von Rubbellosen. Zum einen sollst du hier geeignete Berechnungsterme für bestimmte kumulierte Wahrscheinlichkeiten aufstellen, zum anderen sollst du bei vorgegebenen Berechnungstermen erkennen, welchen Wahrscheinlichkeiten dies im Kontext entspricht. | Arbeitsblatt zum Download | auf  teilen

 m13v0713  Kumulierte Wahrscheinlichkeiten für Binomialverteilungen mit große n-Werten lassen unter Verwendung der Sigma-Regeln abschätzen, wenn das Intervall in der Nähe des Erwartungswertes liegt. So eine Abschätzung soll in dieser Aufgabe gemacht werden. | Arbeitsblatt zum Download | auf  teilen